入試問題にチャレンジ⑨上位校を目指す中3生へ(数学)

1. 図は、正五角形ABCDEであり、頂点Aの位置に2点P、Qがある。点Pは正五角形ABCDEの頂点を、さいころの出た目の数だけ左回りに頂点Aから1ずつ順に動く点である。点Qは正五角形ABCDEの頂点を、さいころの出た目の数だけ右回りに頂点Aから1ずつ順に動く点である。

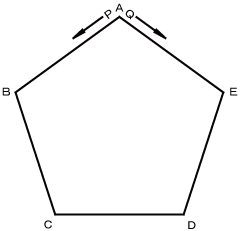
(1) さいころ1つを1回投げて、点Pが動く場合を考える。例えば、出た目の数が3ならば、点Pは頂点Dに止まる。点Pが頂点Bに止まる確率を求めよ。

(2) さいころ2つを同時に1回投げて、出た目の数の和だけ点Pと点Qが動く場合を考える。例えば、出た目の数の和が9ならば点Pは頂点Eに、点Qは頂点Bに止まる。点Pが頂点Cに止まる場合と、点Qが点Cに止まる場合を比べると、どちらのほうが頂点Cに止まりやすいか。点Pが頂点Cに止まる確率と点Qが頂点Cに止まる確率を使って、説明せよ。ただし、確率を求める過程は書かなくてよい。

高知　’17

「2.あきらさんは「数当てのしくみ」について先生と会話した。次の□は、先生と昭さんの考えたことである。ノートは、あきらさんが「数当てのしくみ」について、正しく説明したものの一部である。

会話とあきらさんの考えたこと
先　生: あきらさんの考える数を当ててみせます。十の位の数字より①の位の数字のほうが大きい2けたの自然数を決めてください。
あきら: (37)にしましょう。
先　生: では、十の位の数字と一の位の数字について考えます。まず、十の位を4倍してください。
あきら: (3を4倍して12だ)
先　生: その数に2をたしてください。
あきら: (12に2をたして14だ)
先　生: その数を5倍してください。
あきら: (14の5倍だから70だ)
先　生: その数に、はじめに決めた数の位置の位の数字の2倍を足してください。
あきら: (70に、7の2倍の14をたして84だ)
先　生: では、計算結果はいくつになりのましたか。
あきら: 84です。
先　生: 84ですね。ということは、初めに決めた2けたの自然数は37ですね。
あきら: その通りです。どうしてわかったのですか。
先　生: 実は、この計算結果に、ある特別な計算をすると、初めに決めた2けたの自然数になります。この特別な計算は、計算結果がどんな数でも変わりません。この特別な計算を、文字式を使って考えてみましょう。特別な計算は、例えば「1をたして、2をかける」のような、加法、減法、乗法、除法のうちのいずれか2つを組み合わせた計算方法です。

あきらさんのノート

「数当てのしくみ」

初めに決めた2桁の自然数について、十の位の数字をm、一の位の数字をnとすると、m、nを用いて、初めに決めた2けたの自然数はア□、計算結果はイ□と表せる。これらの文字式を比べると、この計算結果から、はじめに決めた自然数を求めるには、̻🔲という特別な計算をするとよいことがわかる。これは、m、nがどんな数の場合でも成り立つ。実際、84にこのに特別な計算をすると、37が求められる。さらに、他の数字でも同じように求めることができた。

(1) ア□、イ□にあてはまる文字式をそれぞれ書け。

(2) 🔲には、加法、減法、乗法、除法のうちのいずれか2つを組み合わせた計算方法が入る。その計算方法を言葉で説明せよ。

高知　’17

 

解答　1. (1) $\frac{1}{3}$      (2) 【説明】点Pが頂点に止まる確率は、$\frac{2}{9}$    点Qが頂点に止まる確率は、$\frac{7}{36}$  したがって、点Pの方が、点Qより点Cに止まりやすい。

2. (1) ア　10m＋n 　　イ　20m＋2n＋10        (2) 例　10をひいて2でわる。　解説　(2) 20m＋2n＋10=2(10m＋n)＋10となるので、10をひいて2でわると2m＋nとなりはじめの自然数が求められる。