入試問題にチャレンジ⑥上位校を目指す中3生へ(数学)

1. 1から6までの目が出る大小1つずつのさいころを同時に1回投げる。大きいさいころの出た目の数をa、小さいさいころの出た目の数をbとする。(a＋b)をaでわった時のあまりが1となる確率を求めよ。ただし、大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。

 

1.下の図で、4点A,B,C,Dは、点Oを中心とする円の周上にある点で、A,D,B,Cの順に並んでおり、互いに一致しない。点Aと点B、点B点D、点Cと点Dをそれぞれ結ぶ。∠ABD>∠CDBとする。

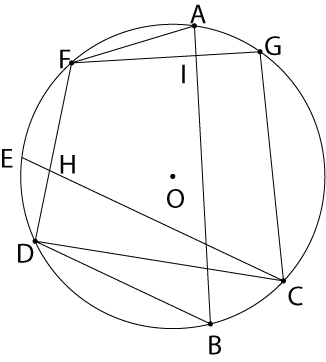
点Cを通り直線BDに平行な直線を引き、円Oとの交点のうち、点Cと異なる点をEとし、点Cを含まない弧AE上に点F、点Bを含まない弧AC上に点Gを、それぞれ弧の両端と一致しないようにとり、点Aと点F、点Dと点F、点Cと点G、点Fと点Gをそれぞれ結び、線分CEと線分DFとの交点をH、線分ABと線分FGとの交点をIとした場合を表している。AB//GCとき、△HCD∽△AFIであることを証明せよ。

 

’20日比谷

解答　1.　　 $\frac{5}{18}$ 

　　大　   1       2        3        4        5        6  左図は、(a＋b)÷aの　余りを表したものである。

小　1    　 0       1        1        1        1        1

小　2        0       0        2        2        2        2

小　3        0       1        0        3        3        3

小　4        0       0        1        0        4        4

小　5        0       1        2        1        0        5

小　6        0       0        0        2        1        0

 

2.線分FAをAの方向に延長した半直線と、線分CGをGの方向に延長した半直線との交点をJとする。△FAIと△FJGにおいて∠AFI=∠JFG (共通) ・・・①　∠FIA=∠FGJ(平行線の同位角) ・・・②　　①、②より　2つの角がそれぞれ等しいので△FAI≡△FJG　また、△FGJと△CDHにおいて、AB//GCより 弧AG=弧BC   CE//BDより　弧BC=弧DE 　したがって、等しい子に対する円周角は等しいから∠GFJ=∠DCH・・・③  四角形FDCGは円に内接する四角形であるから、∠FDC＋∠CGF=180°　∠FGJ＋∠CGF=180°　したがって　∠FGJ=∠HDC・・・④　　　③、④より　2つの角がそれぞれ等しいので　　△FGJ≡△CDH