公立トップ校を目指すあなたへ・・・チャレンジ問題(三平方の定理・相似)

三平方の定理・・・直角三角形において　斜辺をC , 残りの2辺を A, B とすると　C ² = A² ＋ B²

相似な図形・・・相似比(辺の比)が　A : B   のとき　面積比　A² : B²     体積比　A³ : B³  

1.下の図のように、1辺が4cmの立方体ABCD-EFGHにおいて、AD、CDの中点をM、Nとするとき、次の問いに答えなさい。(ラサール ’14改)

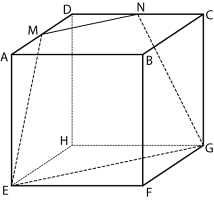
(1) 四角形MEGNの周の長さを求めなさい。

(2) 四角形MEGNの面積を求めなさい。

(3) 平面図形MEGNで、この立体を2つに切ったとき、点Bを含む方の立体の体積を求めなさい。

2.  下の図のように、底面の半径が4cm、母線の長さが16cmの円錐の中に、2つの球A、Bがぴったり収まっています。以下の問いに答えなさい。(城北埼玉　’14)

 

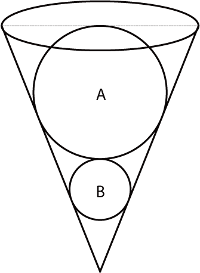
(1) 円錐の高さを求めなさい。

(2) 球Aの半径を求めなさい。

(3) 球Bの半径を求めなさい。

 

 

解答　1. (1) 6√2 ＋ 4√5  (cm)        (2)  18(cm²)               (3)  45$\frac{1}{3}$  (cm³)    

          2. (1) 4√15 (cm)                (2)  $\frac{4}{5}$ √15  (cm)         (3)   $\frac{12}{25}$ √15 (cm)