入試問題にチャレンジ⑪上位校を目指す中3生へ(数学)

1. 1目もりが縦、横ともに1cmの等しい感覚で線が書かれている方眼紙があり、この方眼紙の線に合わせて１辺の長さがncmの正方形の紙を2枚切り取る。この2枚の紙を、重なる部分が1辺の長さ1cmの正方形となるようにはり合わせる。このはり合わせた紙の上に、1辺の長さ1cm正方形の黒いタイルと白いタイルを、次の①、②の方法で順にしきつめ、使われたタイルの枚数を調べることにする。ただし、nは2以上の整数とする。

① はり合わせたとき、上になった1辺の長さがncmの正方形の紙に引ける2本の対角線のうち、重なっている部分を通る方の対角線を引き、それを伸ばした直線を下になった紙に引く。

② ①で引いた線の上には黒いタイルを、それ以外には白いタイルを、方眼紙の線に合わせてすき間なくしきつめる。

 

例　　n=3のとき、
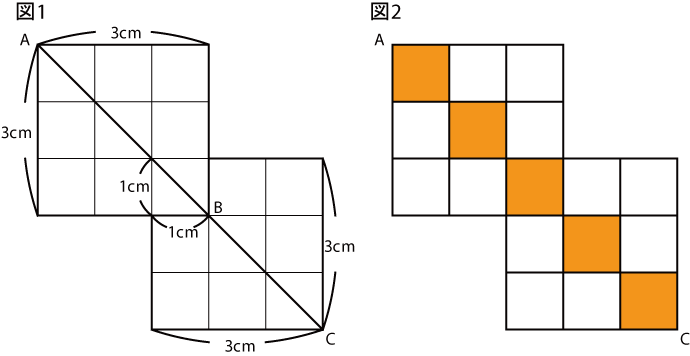
① 下の図のように、はり合わせて上になった正方形の紙に対角線ABを引き、それをCまで伸ばす。
② 図1の線分ACには黒いタイルを、それ以外には白いタイルをしきつめる。この結果、図2k

ようにタイルがしきつめられ、使われた黒いタイルは5マい、白いタイルは12枚である。

このとき、次の問いに答えよ。
(1) n=5のとき、使われた白いタイルの枚数を求めよ。

(2) 使われた白いタイルの枚数が144枚のとき、使われた黒いタイルの枚数を求めよ。

神奈川　’07

 

2. 数学授業で、先生から次の問題が出された。

問題　　6で割ったとき2余る正の整数と、6でわったとき3余る正の整数との積は、どんな数になるだろうか。

(1) みほさんは、どんな数になるか調べるために下の表をつくった。表中のア、イにあてはまる数の組を1つ書け。アにあてはまる数は8より大きい数とする。

(6でわったとき2あまる正の整数 )　　　×          ( 6でわったとき3あまる正の整数 )     =   (積)

2                                     ×　　　　　     　3                   =     6
2                                     ×　　　　           9                   =   18
8                                     ×　　　　　　     3                   =   24
8                                     ×　　　　　　     9                   =   72
ア  □                               ×　　　　　        3                   =   イ□

(2) みほさんは、(1)で調べたことから、「6でわったとき2余る正の整数と、6でわったとき3余る正の整数との積は、いつも6の倍数である。」と予想し、その予想が正しいことを次のように証明した。みほさんの証明を完成せよ。

証明　6でわったとき2余る正の整数を6m＋2と表す。ただし、mは0以上の整数とする。

 

 

したがって、6でわったとき2余る正の整数と、6でわったとき3余る正の整数との積は、いつも6の倍数である。

難(3) みほさんが(2)で証明した数の性質をもとに、正の整数a、b、cについて次の事柄が成り立つかどうか考えた。

a でわったとき b 余る正の整数と、a でわったとき c 余る正の整数との積は、いつも a の倍数である。

よし子さんが考えたことについて、

① b が4、c が6のとき、下線のことがらが成り立つような a にあてはまる数は3つある。そのうちの1つが24である。a にあてはまるほかの2つの数を求めよ。

② a が 7 のときは、その余りである b と c にどんな数をあてはめても、下線のことがらが成り立たない。このように、下線のことがらが成り立たない a のうち、20以下の2けたの数をすべて求めよ。

岐阜　’14

 

解答　1. (1)  40枚　　(2)  17枚

解説
1. (1)  タイルの総数は、5² ×2=50 (枚)　重なっているのが1枚。→  50-1=49 (枚)
黒のタイルの数は5×2=10 (枚) 重なっているのが1枚  →10－１=９ (枚)
したがって、49－9=40  (枚)
2. (2) 正方形の1辺の長さが n cmのとき、
黒いタイルの数は、 2n－1 (枚) 、白いタイルの枚数は、(2n²－1)－(2n－1)= 2n²－2n  (枚)
したがって、 2n²－2n=144   2n(n-1)=144    n²－n－72=0  (n＋8)(n－9)=0
n≧2より　n=9 黒いタイルは、2×9－1=17 (枚)

2.  (1) ア　14    イ　42
(2)  6で割ったとき 2余る正の整数を6m＋2と表す。ただし、mは0以上の整数とする。 6で割ったとき 3余る正の整数を6n＋3と表す。ただし、nは0以上の整数とする。
この2数の積は、(6m＋２)(6n＋3)=36mn＋18m＋12n＋６=６(６mn＋3m＋２n＋1)　ここで、６mn＋3m＋２n＋1　は整数だから　６(６mn＋3m＋２n＋1)は6倍数である。
(3) 8、12       (4)  11 , 13 , 17 , 19

解説　(1)  ア　6×2＋2=14   イ  14×3=4
(3) ①　M、Nを0以上の整数とすると、この2数は、aN＋b (0≦b＜a),aM＋c (0≦c＜a)と表される。したがって、この2数の積は、(aN＋b)( aM＋c)=a²MN＋abM＋caN＋bc=a ( aMN＋bM＋cN )＋bc
b が4、c が6のとき　この2つ整数は、aN＋4 (0≦4＜a) , aM＋6 (0≦6＜a) と表される。この2数の積は、(aN＋4)( aM＋6)=a²MN＋4aM＋6aN＋24=a(aMN＋4M＋６N)＋24
したがって、aは7以上の24の約数である。8、12、24    答　8、12

②  ①より、aはbcの約数で、0≦b＜a) , 0≦c＜aを満たすとき、2数の積はaで割り切れる。ここで、これが成り立たないのは、bcが素数のときである。(bcが素数のとき、aがその数の約数になるとrすると、bまたはcのどちらかがその素数となり、aでわったときのの余りとなることはない。したがって、a= 11 , 13 , 17, 19